Blog

Problem link

আলোচনাঃ

      আমাদেরকে একটা Trapezium দেয়া হবে। তার ক্ষেত্রফল বের করতে হবে।

উত্তরঃ

আমরা জানি, Trapezium এর ক্ষেত্রফল = 0.5*( সমান্তরাল বাহুদ্বয়ের যোগফল * উচ্চতা )

আমাদের সমান্তরাল বাহুদ্বয়ের মান দেয়া আছে । শুধু উচ্চতা বের করলেই হলো। তো এটা দুইভাবে করা যায়।

1)

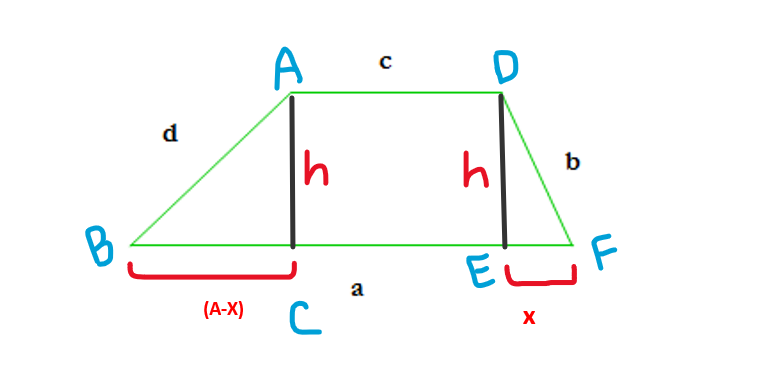
Trapezium ABFD তে AB এর সমান করে DE বাহু আকি। তাহলে ADBE সামান্তরিক তৈরি হলো। এখন , AD = BE and AB = DE. So, BE = c , DE = d

and EF = a-c = x . ধরি DK = h

△DEF হতে পাই,

=> s = (DE+EF+DF)/2

SO, Area of △DEF = sqrt(s*(s-DE)*(s-EF)*(s-DF))

                             = sqrt(s*(s-d)*(s-x)*(s-b)

আবার আমরা জানি,  △DEF= 0.5*EF*DK

                                          = 0.5*x*h

তাহলে আমরা লিখতে পারি,

          0.5*x*h = sqrt(s*(s-d)*(s-x)*(s-b))

    So, h = ( sqrt(s*(s-d)*(s-x)*(s-b)) * 2) / x

2)

আমরা a এর উপর দুইটা লম্ব টানবো ।  লম্ব টানার পর একটা অংশকে যদি x ধরি তাহলে অপরটা হয় (a-x). তাহলে দুইটা সমকোণী ত্রিভুজ তৈরি হলো।

△ABC থেকে পাই,

       Here, big= (a-c)

       d^2 = (big-x)^2 + h^2 ———-(1)

△DEF থেকে পাই,

       b^2 = h^2 + x^2

  =>h^2 = b^2 – x^2 ————–(2)

From (1),

    d^2 = (big-x)^2 + h^2

=>d^2 = (big-x)^2 + b^2 – x^2

=>d^2 = big^2 + x^2 – 2*big*x  + b^2 – x^2

=>d^2 = big^2 – 2*big*x  + b^2

SO, x = (big^2 + b^2 – d^2) / (2*big)

So, h = sqrt(b*b – x*x)

C++ Code:

#include<bits/stdc++.h>
using namespace std;
#define PI acos(-1.0)

int main(){
    int t;
    cin>>t;
    double a,b,c,d;
    for(int i=1;i<=t;i++){ // O(1)
        cin>>a>>b>>c>>d;
        double x=abs(a-c);
           
        double s=(x+b+d)/2.0;
        
        double triangleArea=sqrt(s*(s-b)*(s-d)*(s-x));
       
        // .5*x*h = triangleArea
        double h=(triangleArea*2)/x;
        double trapeziumArea=.5*(a+c)*h;
        
        printf("Case %d: %.10f\n",i,trapeziumArea);
    }
}

-----------------------------------  OR ------------------------------------

#include<bits/stdc++.h>
using namespace std;
#define PI acos(-1.0)
int main(){
    int t;
    cin>>t;
    double a,b,c,d;
    for(int i=1;i<=t;i++){
        cin>>a>>b>>c>>d;
        double big=abs(a-c);
        double x=(b*b + big*big - d*d)/(2*big);
           
        double h=sqrt(b*b-x*x);
        double trapeziumArea=.5*(a+c)*h;
       
        printf("Case %d: %.10lf\n",i,trapeziumArea);
    }
}